Pourquoi est-il préférable d’éviter l’enseignement des trucs en mathématiques?
Introduction
Il existe une tonne de trucs et de raccourcis mathématiques qui visent à rendre les calculs et la résolution de problèmes mathématiques plus efficaces et rapides. On parle d’un truc mathématique pour désigner une méthode utilisée de façon mécanique, souvent basée sur la mémorisation, sans compréhension (Adihou et Marchand, 2010). On y retrouve un aspect presque magique : on ne sait pas expliquer pourquoi cela fonctionne.
La problématique des trucs
En effet, l’enseignement de trucs mathématiques peut nuire à la compréhension des élèves, car ceux-ci limitent le développement de la compréhension conceptuelle. La compréhension conceptuelle fait référence notamment au sens du nombre, au sens des opérations et au sens de la fraction. Les trucs ont tendance à court-circuiter ces derniers en évacuant les bases sur lesquelles ils s’appuient. Par ailleurs, les trucs évacuent également fréquemment le langage mathématique. Enfin, si les trucs peuvent parfois simplifier la vie de nos élèves lorsqu’on les enseigne, ils entravent fréquemment la compréhension de concepts ultérieurs.
Par contre, il est possible et souhaitable d’amener les élèves à construire leurs propres raccourcis mathématiques au fil du temps. Lorsque les élèves ont des bases conceptuelles solides, ils découvriront ces fameux trucs sans doute par eux-mêmes et sauront expliquer le raisonnement derrière ceux-ci. C’est ce qu’on appelle la généralisation. Cette dernière permet aux élèves d’utiliser les raccourcis découverts dans des problèmes de plus en plus complexes.
Multiplier par 10 en ajoutant un zéro
Lors de l’apprentissage des tables de multiplication, il est assez fréquent que l’on fasse observer aux élèves que, pour la table du 10, il suffit d’ajouter un 0 à la fin du nombre. Cela permet de mémoriser facilement plusieurs faits mathématiques. Par contre, il existe une lacune importante avec ce truc : il n’est tout simplement pas vrai. En effet, lorsqu’on multiplie un nombre décimal par 10, il ne suffit pas d’ajouter un 0 à la fin. Il s'agit également de la même chose lorsqu’on multiplie des fractions par 10.
Or, il deviendra plus difficile de déconstruire ce truc lors de l’enseignement de ces concepts que de tout simplement l’éviter dans un premier temps. Il serait préférable d’explorer la logique de cette régularité avec les élèves. Notre système de numération positionnelle est en base 10.
Cela signifie que chaque groupe de 10 correspond à une dizaine qui se représente par le chiffre 1 à la position des dizaines. Ainsi, lorsqu’on multiplie 5 par 10, on se retrouve avec 5 groupes de 10 unités ou avec 5 dizaines. Il en va de même pour 523 x 10 qui équivaut à 523 dizaines qui s’écrit 5 230. Cette explication permet de renforcer la compréhension du système de numération positionnelle des élèves. De la même manière, lorsqu’on multiplie 4 dixièmes (0,4 ou 4/10) par 10, on se retrouve avec 4 groupes de 10 dixièmes ou 4 unités que l’on écrit 4. Pour aider à illustrer ce raisonnement, du matériel de manipulation de base 10 et un tableau de numération peuvent être utilisés.
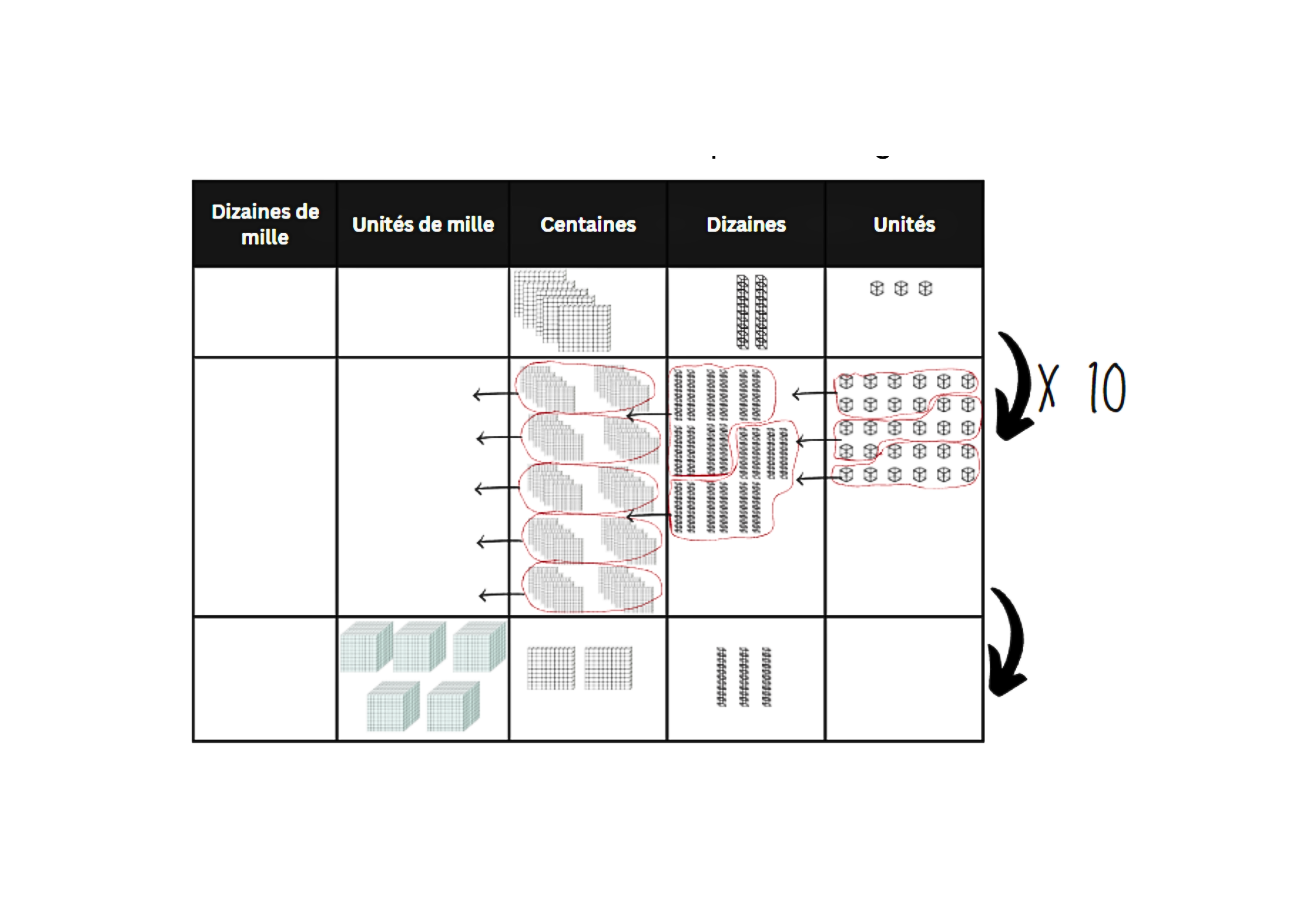
Déplacer la virgule pour transformer les unités de mesure
Il est souvent enseigné aux élèves que, pour transformer une mesure présentée dans une unité de mesure comme les centimètres en une autre, il suffit de déplacer la virgule vers la gauche ou la droite autant de fois qu’il existe d’unités entre celle de départ et celle désirée. Ainsi, pour transformer 250 centimètres en mètres, il faut déplacer 2 fois la virgule vers la gauche pour obtenir 2,5 m. Or, ce truc peut causer de nombreuses confusions chez les élèves. Il est en effet fréquent que l’élève se confonde dans le sens du déplacement de la virgule ou dans le nombre de déplacements nécessaires. De plus, ce truc s’appuie lui aussi sur une fausseté : en réalité, ce n’est pas la virgule qui se déplace, mais bien les chiffres.
La virgule, quant à elle, est toujours située au même endroit : entre les unités et les décimaux.
Pour mieux faciliter la compréhension du système international d’unités, il est essentiel que les élèves aient une connaissance claire de ce que représente chaque unité de mesure. Il vaudrait donc faire manipuler et mesurer les élèves afin qu’ils comprennent bien qu’un millimètre est plus petit qu’un centimètre, etc. Ainsi, il sera beaucoup plus facile de s’appuyer sur ces connaissances pour transformer les unités de mesure : si un millimètre est plus petit qu’un centimètre, il y en entre forcément beaucoup plus dans une mesure donnée.
Le produit croisé
Le produit croisé (parfois aussi appelé la méthode du poisson, du papillon ou de la roue) est un truc utilisé pour résoudre rapidement des calculs liés aux fractions équivalentes. Or, plutôt que de renforcer la compréhension de l’équivalence et de la proportionnalité, cette méthode nuit au développement de ces concepts essentiels. Encore une fois, on y favorise la mémorisation d’une procédure en dépit de la construction de sens. Par ailleurs, si on ne comprend pas pourquoi cela fonctionne, les risques de se tromper en l’appliquant deviennent beaucoup plus grands : additionner plutôt que multiplier, ne pas utiliser les bons nombres, etc.
En construisant un bon sens de la fraction dès les premiers apprentissages, il devient beaucoup plus facile d’encourager les élèves à s’appuyer sur ce raisonnement pour trouver des fractions équivalentes.
Dans un premier temps, il est intéressant d’utiliser du matériel de manipulation ou des outils visuels comme la double droite numérique pour observer le rôle du numérateur et du dénominateur dans les fractions équivalentes. Ensuite, pour faciliter les calculs, on préfèrera enseigner le retour à l’unité ou encore le facteur de changement.
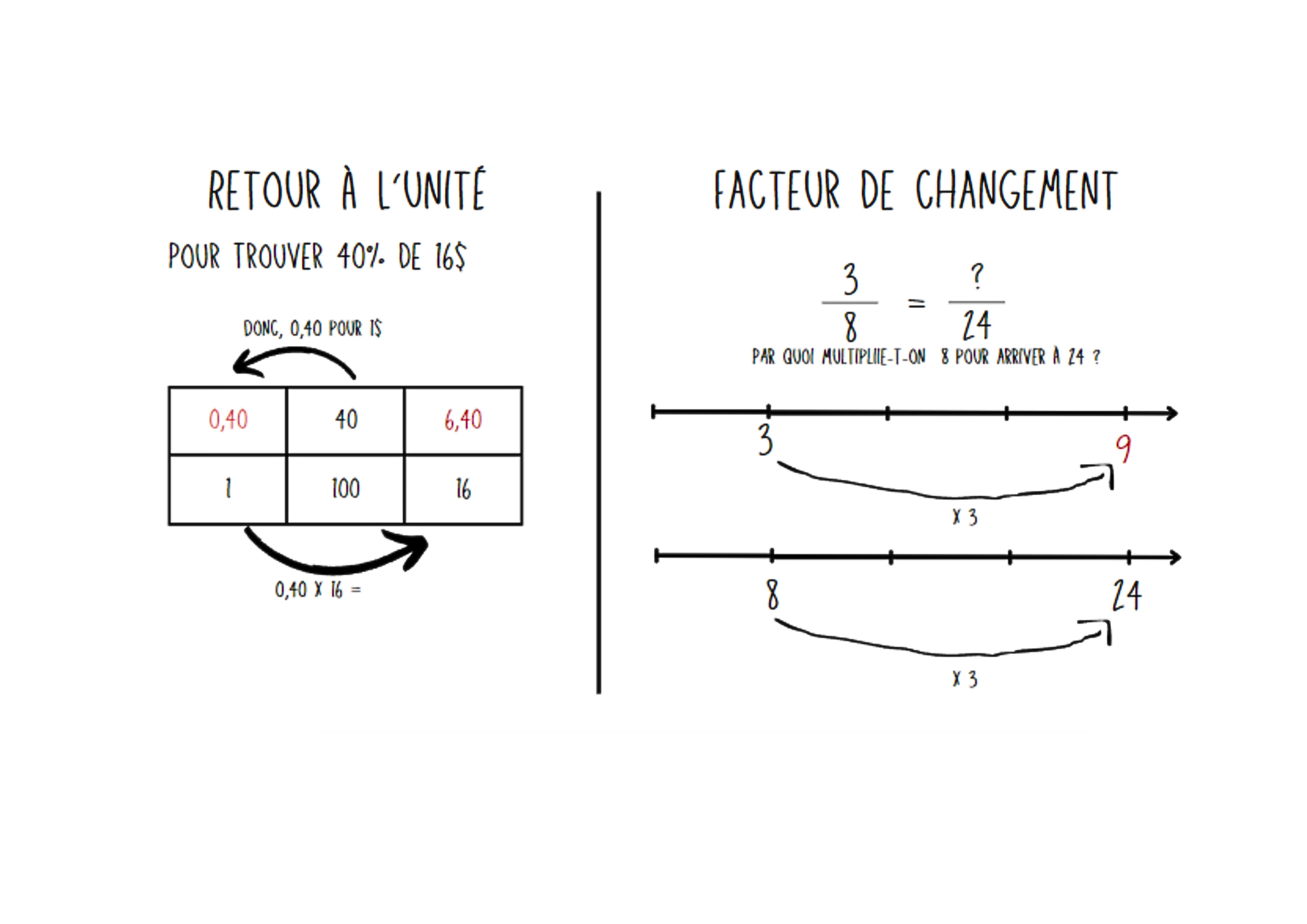
Pour aller plus loin
Adihou, A. et Marchand, P. (2018). Les trucs mathématiques au primaire : et si on leur donnait du sens! Editions JFD.
Adihou, A. et Marchand, P. (2010). Trucs mathématiques. Bulletin AMQ, 50(3), p. 38.
Un peu plus sur l'autrice
Jeanne Larocque-Jeffrey a obtenu son baccalauréat en adaptation scolaire et sociale de l’UQAR en 2017. Depuis, elle a travaillé comme orthopédagogue dans différents milieux : en centre jeunesse, en clinique privée et dans des écoles secondaires publiques. Parallèlement à ceci, elle a réalisé une maitrise en adaptation scolaire et sociale à l’Université de Sherbrooke cherchant à documenter les pratiques rapportées avec les élèves ayant des troubles de comportement ainsi que les attitudes des orthopédagogues à leur égard. Elle se passionne pour les pratiques d’enseignement basées sur les données probantes.











.png)


