Vivre la résolution de problème autrement? Faites place aux tâches découpées!
Introduction
Deux heures viennent de s’écouler! Dans la classe, certains élèves s’occupent en silence depuis une heure, d’autres sont en voie de terminer. L’enseignante est entourée d’un sous-groupe qui n’arrivera pas au bout de la tâche malgré un soutien important. La cloche sonne et l’enseignante songe : « La résolution de problème, c’est beaucoup trop complexe pour mes élèves! » Pourtant, l’essence même du programme de formation en mathématique s’inscrit dans une approche par la résolution de problèmes. Il faut donc porter notre réflexion sur les types de tâches que nous proposons à nos élèves et non sur la résolution de problèmes en soi. Souhaiteriez-vous vivre autrement vos tâches classiques de résolution de problème? Laissez-vous charmer par les tâches découpées!
La résolution de problème, essentielle, complexe, mais pas compliquée!
Pour certains élèves, les tâches de résolution de problèmes qui s’apparentent à celles imposées par le ministère à la fin du 3e cycle du primaire sont un véritable casse-tête.
Beaucoup d’enseignants soulignent que les élèves :
semblent perdus devant la quantité d’informations à traiter;
éprouvent de la difficulté à s’organiser dans leur démarche;
sélectionnent difficilement les bonnes données à traiter.
Pourtant, le Programme de formation de l’école québécoise, le Référentiel d’intervention en mathématique ainsi que plusieurs didacticiens dans le domaine placent la résolution de problème au cœur de l’activité mathématique. À la suite de ces constats, il va de soi que l’ajustement des pratiques pédagogiques est nécessaire pour favoriser une meilleure progression de la compétence des élèves en mathématiques.
Le traitement de situations-problèmes est omniprésent dans les activités mathématiques. En tant que processus, la résolution de situations-problèmes constitue un objet d’apprentissage en soi. En tant que modalité pédagogique, elle supporte la grande majorité des démarches d’apprentissage en mathématiques. (PFEQ, p. 124)
Comment puis-je amener mes élèves à développer leur compétence dans l’organisation ou la sélection des données utiles?
Quelques solutions sont envisageables.
Proposer différents types de tâches aux élèves.
Favoriser la collaboration et la communication entre les élèves.
Questionner les élèves pour accéder à leur raisonnement, pour faire évoluer leur réflexion et leurs connaissances en mathématiques.
Engager les élèves dans de véritables situations de résolution de problème.
L’expérimentation des tâches découpées dans différentes classes nous a permis d’intégrer dans nos pratiques pédagogiques plusieurs de ces pistes de solution.
Les tâches découpées sont une autre manière de présenter les tâches plus classiques de résolution de problèmes. Par « classique », nous entendons des tâches de résoudre (compétence 1) ou de raisonner (compétence 2) généralement présentées sous les formes suivantes :
Mise en situation sous forme de texte.
Présentation des données sous différents modes de représentation (symboles, diagrammes, tableaux, données numériques, etc.).
La procédure est simple. Il s’agit, tout simplement, de découper la tâche en plusieurs bandelettes :
Une première bandelette pour introduire le contexte et la question.
Les autres bandelettes seront découpées en fonction de la disposition des indices et des données utiles à la résolution de problème. Par exemple : un tableau de données sur une bandelette, une information qui précise le nombre de fleurs dans un jardin, etc.
Puis-je ajuster n’importe quel problème écrit en tâches découpées?
Bien entendu! Parfois, vous aurez à modifier la disposition des informations pour faciliter le découpage, mais toutes formes de problèmes écrits peuvent être transformées en problèmes découpés. Il s’agit d’une bonne piste pour dynamiser votre enseignement et pour enrichir les problèmes proposés dans vos manuels scolaires.
L’objectif de ce type de tâche est de ne pas dévoiler d’un seul coup les informations et les données du problème aux élèves. C’est par leurs réflexions et leur analyse de la situation de départ qu’ils arriveront à réfléchir réellement aux données pertinentes qui leur permettront de résoudre le problème. Une fois l’activité lancée, cela relève de la responsabilité des élèves de planifier, de recueillir l’information et de traiter les données. Telle une mission à accomplir, les tâches découpées favorisent l’engagement de tous les élèves!
Deux astuces avant de vous lancer
Une tâche découpée se vit en collaboration. Une importance est accordée aux échanges et au soutien entre les élèves. Il est donc suggéré de placer les élèves en dyade ou en triade.
Est-ce que les groupes doivent être homogènes ou hétérogènes?
Bonne question! Cela dépend de votre intention d’apprentissage. Toutefois, la composition des groupes devrait permettre à tous les élèves de contribuer à la réflexion et à la démarche de résolution de problème, et ce, en fonction de ses connaissances actuelles des concepts et processus visés par la tâche.
Vivre une tâche découpée modifie la posture de l’enseignante en regard de l’accompagnement à offrir aux élèves. Dans ce contexte, ce sont les élèves qui prennent en charge l’analyse du problème et la planification des étapes à franchir pour le résoudre. L’enseignante, pour sa part, guide et questionne les élèves pour les soutenir dans leur analyse.
Finalement, les élèves doivent travailler davantage que l’enseignante!
Vers un ajustement de la posture de l'enseignante
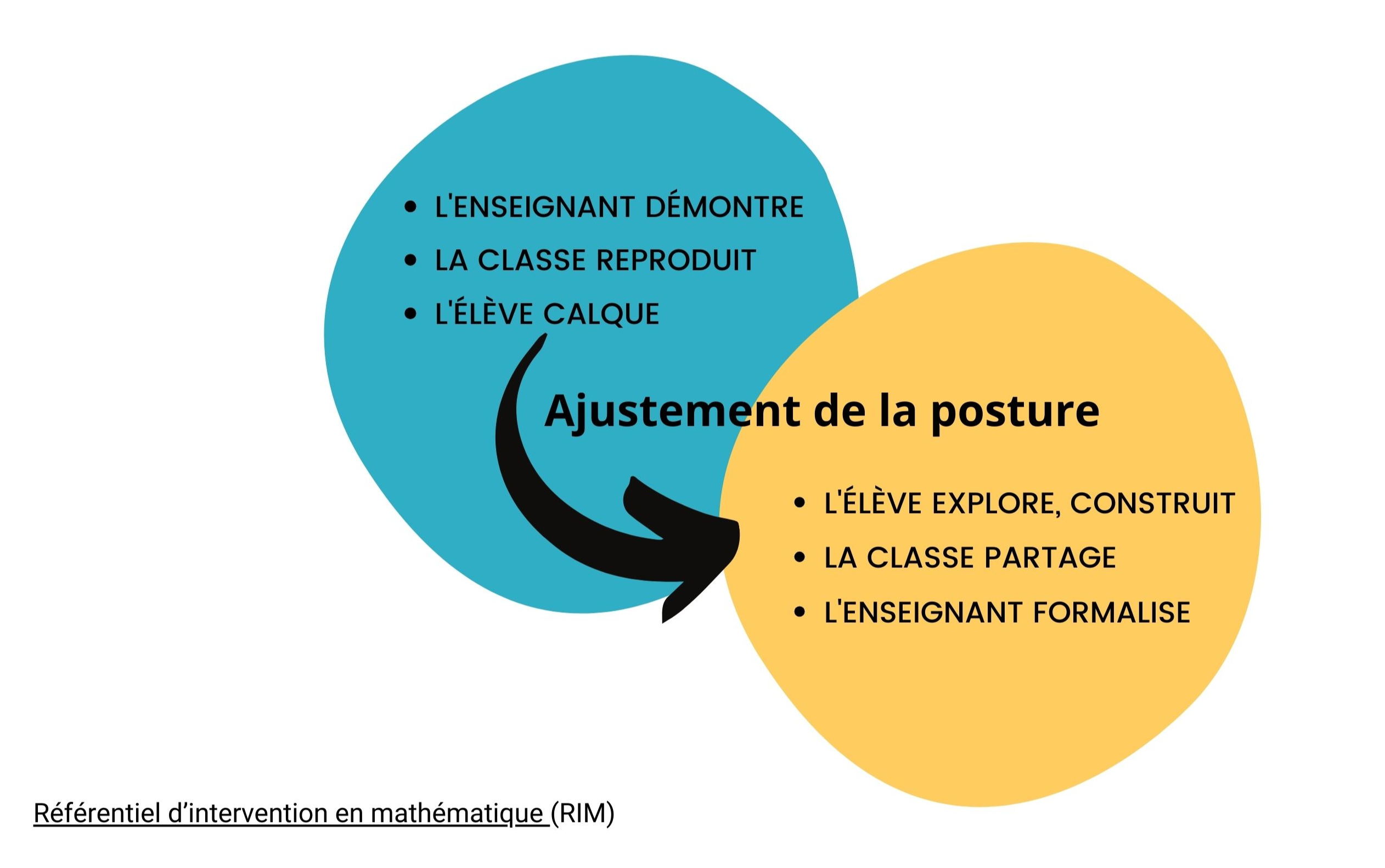
Inspiré du Référentiel d’intervention en mathématique (RIM)
Comment vivre une tâche découpée avec mes élèves?
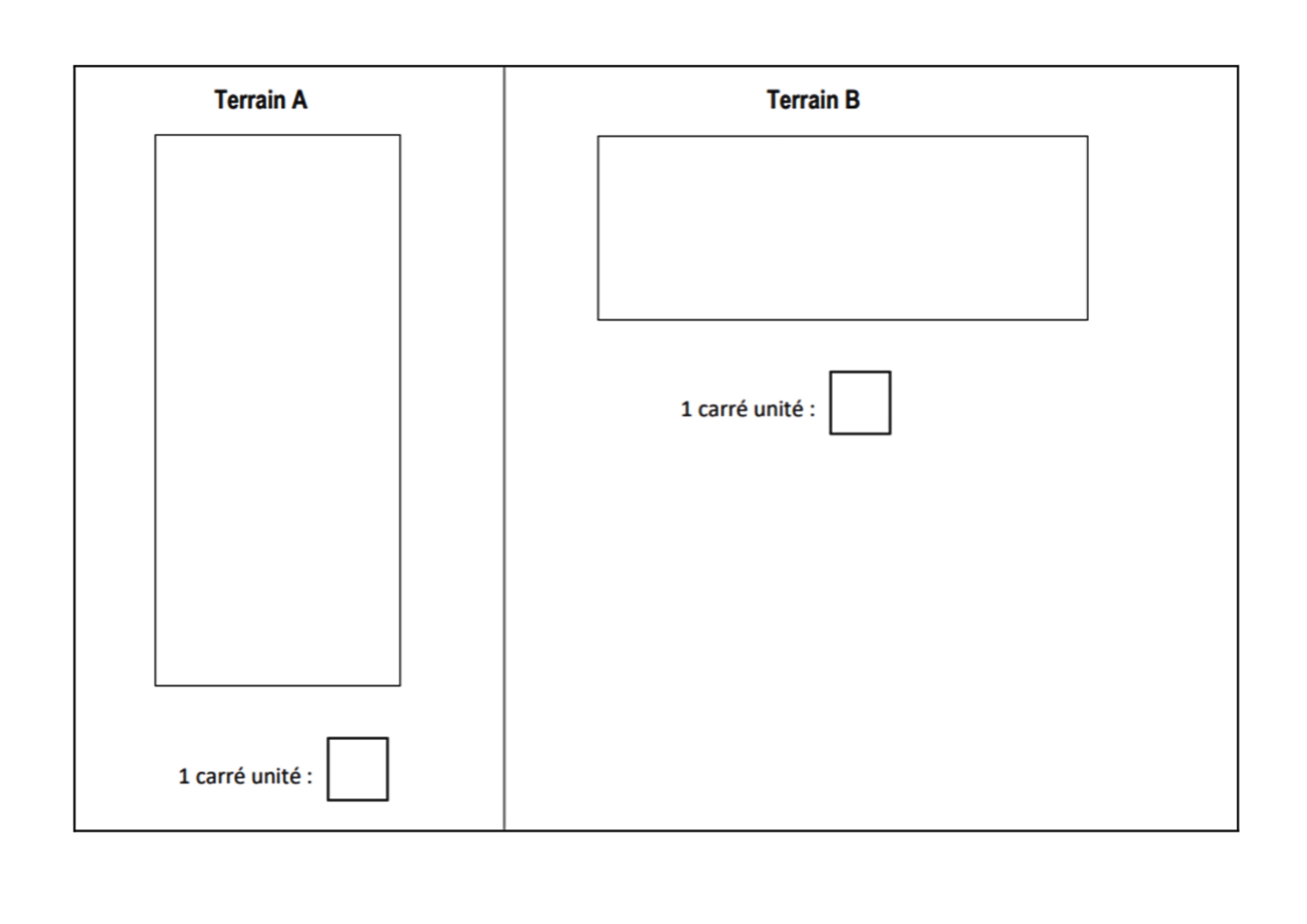
Les terrains de soccer
Deux équipes de soccer veulent jouer une partie. Ils hésitent entre deux terrains, car ils ne savent pas laquelle satisfait leur critère de sélection.
Quel terrain les deux équipes choisiront-elles pour jouer leur partie?
Étape 1 : Remise de la mise en situation et de la question aux élèves.
Dès la réception de la première bandelette (voir encadré ci-haut), les équipes sont amenées à se questionner sur les informations dont elles auront besoin pour résoudre le problème. Les élèves sont rapidement mobilisés dans une démarche réflexive de résolution de problème. Afin de pouvoir avoir les informations, ils doivent demander à l’enseignante l’information précise qu’ils désirent recevoir et la raison pour laquelle les élèves en ont besoin.
Exemple : « Nous aurions besoin de connaitre les dimensions des deux terrains de soccer pour pouvoir les comparer. »
C’est à ce moment que l’enseignant.e remet une bandelette de papier à l’équipe avec l’information dont celle-ci a besoin.
Étape 2 : L’équipe est invitée à commencer à résoudre le problème.
L’enseignant.e propose un support qui permettra aux élèves de consigner les traces de leur démarche : cahier, feuille brouillon, matériel de manipulation, etc. À cette étape, les élèves n’auront pas tout en main pour résoudre la situation problème. C’est tout l’intérêt de résoudre des problèmes en tâche découpée!
Étape 3 : Questionnement de l’équipe : « D’autres informations sont-elles nécessaires pour résoudre la tâche? »
Une fois cette analyse réflexive effectuée, les équipes demandent et justifient à l’enseignant.e les données qu’ils jugent pertinentes pour poursuivre leur démarche. Les allers-retours se poursuivent jusqu’à ce que les équipes aient rassemblé toutes les données pertinentes et qu’elles aient appliqué les concepts et processus requis par la situation.
Étape 4 : Présenter et partager les démarches et les stratégies et comparer leurs solutions en groupe
Cette étape est importante dans le développement des compétences en mathématiques. Par ses traces claires et complètes et par le partage de sa solution, l’élève nous démontre sa façon pour arriver à résoudre le problème. Ainsi, les élèves sont exposés à différentes stratégies et l’enseignant.e profite de ses observations pour formaliser ou ajuster certains concepts et processus.
Une dernière astuce : Lancez-vous en collaboration avec vos collègues, l’orthopédagogue et, surtout, faites confiance à vos élèves!
Un exemple de tâche découpée

Tâche adaptée à des situations créées en 2015-2016 par des conseillers pédagogiques et par des enseignants dans le cadre d’un projet régional rendu possible par les fonds coopératifs (03-12).
Pour aller plus loin
Récit MST.(2021). Apprendre et évaluer autrement en mathématiques.
Goulet, M.-P. et Voyer, D. (2023). L’utilisation de la méthode « ce que je sais, ce que je cherche » en classe de mathématiques : analyse de productions d’élèves. Revue deMathématiques pour l’école (RMé), 239(1), 3-15, https://www.rme.swiss/article/view/3797/3462
Goulet, M.-P, (2023). CVCRDM Marie-Pier Goulet.
La recherche en didactique des mathématiques; Une création du CVCRDM (Comité de valorisation et de communication des recherches en didactique des mathématiques). Étude de méthodes de résolution de problème écrit de mathématiques présentées au primaire : Pratique associées et effets des ces méthodes sur l’activité mathématique des élèves.
Ministère de l’éducation et de l’enseignement supérieur du Québec. (2018). Programme de formation de l’école québécoise. Repéré à http://www.education.gouv.qc.ca/enseignants/pfeq/
Ministère de l’Éducation et de l’Enseignement supérieur du Québec. (2019). Référentiel d’intervention en mathématique. Québec : Gouvernement du Québec.Repéré à https://www.education.gouv.qc.ca/fileadmin/site_web/documents/dpse/adaptation_serv_compl/Referentiel-mathematique.PDF
Ministère de l’Éducation et de l’Enseignement supérieur du Québec. (2009). Progression des apprentissages en mathématique. Repéré à https://www.education.gouv.qc.ca/fileadmin/site_web/documents/education/jeunes/pfeq/PDA_PFEQ_mathematique-primaire_2009.pdf
Un peu plus sur l'autrice
D’orthopédagogue à conseillère pédagogique, Marie-Ève Guérin travaille depuis 16 ans auprès des élèves à besoins particuliers. Elle est bachelière en adaptation scolaire et elle a aussi réalisé un DESS en éducation ayant pour sujet l’utilisation de la littérature jeunesse et la différenciation pédagogique. Au fil des ans, elle a développé une expertise dans la mise à place de modèle de service collaboratif tel que le coenseignement. Au cours des 3 dernières années, son rôle de conseillère pédagogique mathématique en inclusion scolaire lui a permis d’expérimenter plusieurs tâches et dispositifs d’enseignement-apprentissage des mathématiques auprès d’une diversité d’élèves. Finalement, elle a découvert que la résolution de problème, ce n’est pas si complexe!











.png)


